PLL に 用いる プログラマブル・デバイダ

2MPCNote

あらまし  周波数シンセサイザー PLL 回路 の応用範囲は、プログラマブル・デバイダの動作 スピードの向上と ともに 拡大しているとも言える。
筆者が スペアナ の設計を始めたころ 1980年初頭には 分周 IC は 数百 MHz が限度で、数 GHz の分周には 温度変動によって 不良分周 を 引き起こす トンネル・ダイオード を用い たりして 苦労したが、現在では プリスケーラ を含めた 安価な 通信機用 PLL IC チップの中に収められている。
そして、この PLL IC に用いられている プログラマブル・デバイダ は ２(デュアル) モジュラス・プリスケーラ 方式、または パルス・スワ ロ 方式 とも 呼ばれるものが 現在 主流となっている。
（正確にはデュアル・モジュラス・プリスケーラを用いたプログラマブル・カウンタでパルス・スワロ・カウンタと 呼ばれ，パルス・スワロ方式のPLL周波数シンセサイザと言う)。

ここでは、２(デュアル) モジュラス・プリスケーラによる パルス・スワロ・カウンタ の 動作原理を示し、その特徴を把握する。
また、パルス・スワロ・カウンタ の総合分周比 Nt を得るための P , A , N カウンタの値を求める 計算式 及び 簡単 な 計算ツール を 提供する。

■　1.  ２モジュラス・プリスケーラによるパルス・スワロ・カウンタの動作説明

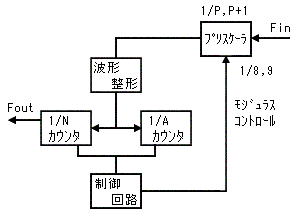
図-1.  ２モジュラス・プリスケーラによるパルス・スワロ・カウンタの構成図

図-1. には、２モジュラス・プリスケーラによるパルス・スワロ・カウンの構成を示す。。

ここで、カウンタ の動作を示すと、

�@  プリスケーラ は 始め 入力周波数 Fin を P + 1 で分周する。

�A  プリスケラー出力は、A カウンタ と N カウンタ 両方に入力され、A個の入力で　A カウンタ は ゼロに なる。  →  ( P + 1 ）A

そして、この時 プリスケーラの 分周比 を P に 切り換える出力を出す。  (モジュラス・コントロール)

�B  さらに N カウンタ は、プリスケーラからの入力で  カウント・ダウンを 続け N カウンタ を ゼロに するま で行なわれる。  →  ( N - A ）P

�C  N カウンタ が ゼロになったら、プリスケーラの 分周比は 再び ( P + 1 ) に戻り、A 及 び N カウンタ も 初期値に戻される。

ゆえに、トータル分周比 N t は 次式で表せる。

	N t ＝ ( P + 1 ）A + P ( N - A )
	＝ N × P + A

なお、ここで 動作原理上      N ≧ A       の条件が必要となる。

■　2.    ２モジュラス・プリスケーラによるパルス・スワロ・カウンタの動作具体例

２モジュラス・プリスケーラによるパルス・スワロ・カウンタは 今では PLL IC の中に組み込まれているので、ディスクリート で構成することは あ まり なくなったが、その 動作原理 を理解することによって 様々な 使い方ができると考えている。
ここで、実際の例 を用いて説明し、その 特徴 を記す。

図-1. の２モジュラス・プリスケーラによるパルス・スワロ・カウンタの構成で 入力周波数 Fin を 1/42 する場合を 考える。
ここで プリスケーラ P = 8    , 1/8  or  1/ (8+1)  の前置分周器とすると、まず 最初の状態として P カウンタ は 1/9 , A カウンタ は 1/2 , N カウン タ は 1/5 に 設定される。

入力信号が 入ってきて P カウンタ で カウントされ 9 カウントされて、P カウンタ から キャリーが出力される。     すると A カウンタ と N カウンタ の値が 一つ減る。
このようにして 入力が次々と カウントされて A カウンタの値が ゼロ になると、A カウンタ から P カウンタ の 分周比を 1/8 にす る 切換え信号が出される。  (モジュラス・コントロール)

入力信号は この時点で 9×2 = 18 パルス 入力されており、N カウンタ は 5 - 2 = 3 になっている。

P カウンタ は N カウンタ の値が ゼロ になるまで 1/8 分周の動作を行い 3×8 = 24 個のパルスを カウントした後に N カウンタ の値が ゼロ に なり、出力が出ると 同時に A カウンタ と N カウンタ 自身に 入力データを プリセットして最初の状態に戻り、この動作を 繰り返して行くことになる。

ゆえに、入力パルスが 18 + 24 = 42 個 入力された時に 出力パルス が １個 出力されることになり、1/42 に 分周 される。

  すなわち、トータル分周比 N t は

	N t ＝ N × P + A
	42 ＝ 5 × 8 + 2

式 の 如くとなる。

  では 次に、トータル分周比 N t = 46 の 場合を見てみる。

	N t ＝ N × P + A
	46 ＝ 5 × 8 + 6

式で 与えられるが、N カウンタ と A カウンタ の関係が N ≧ A　を満足していない。

動作原理上 N カウンタ は A カウンタ から P カウンタ を 切換える出力が だされる前に ゼロ になってはならないことから　N t = 46 の 設定はできない、動作しないことになる。
このことは、デュアル・モジュラス・プリスケーラ カウンタ を用いる時に 注意を要する ことである。

下の 表-1. には 1/8 , 1/9 の プリスケーラ カウンタ を使用したときの 各々の トータル分周比 N t を得 るための A カウンタ と N カウンタ の値を 記した。

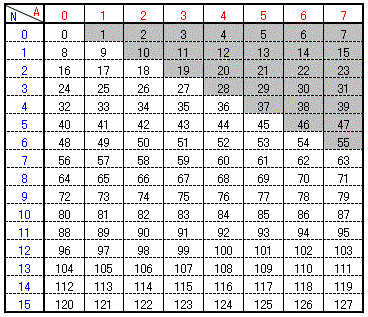
表-1.  プリスケーラ 1/8 , 1/9 を使用した時の A カウンタ と N カウンタ の値

灰色 で 塗りつぶした部分は、A カウンタ の値が N カウンタ の値より大きくなる場合で 設定が不可能な トータル分周比 N t で ある。
もし、N t を 1 STEP づつ増やして 連続して用いる仕様であれば、56 以上の 分周比 からで ないと 用いることができないことになる。

■　3.  デュアル・モジュラス・プリスケーラ PLL の 各 カウンタ 値を求める 計算ツール

以下に PLL の プログラマブル・デバイダ に ２モジュラス・プリスケーラによる パルス・スワロ・カウンタ を用いた時の 各 カウンタ の 値 を求め る 計算ツール を設置する。

ここで、PLL の 比較周波数 REF と 出力周波数 OUT 及び プリスケーラ カウンタ P の値を 入力すると、トータル分周比 Nt を求 め 次に 必要な N カウンタ , A カウンタ の値を 算出してくれる もの とした。

2mpcCalc		OUT ：  Hz KHz MHz
REF ：  Hz KHz MHz		P =

	Nt =

	Nt = ×＋	ただし、N ≧ A
	Nt = ×＋

 では、比較周波数 REF = 12.5 KHz で 出力周波数 OUT = 420.5 MHz そして プリスケーラ P = 256 とした場合であるが、ここ で START ボタン を押すことにより トータル分周比 Nt = 33640 で N = 131　そし て A = 104 が求まる。    ゆえに この N 及び A の値を設定することにより ２モジュラス・プリスケーラによる パルス・ スワロ・カウンタ は トータル分周比 Nt = 33640 で作動することになる。

次に、出力周波数を OUT = に変更する。
START ボタン を押すことにより トータル分周比 Nt = 33672 で N = 131　そし て A = 136 と求まるが、N ≧ A の 条件外 となり この設定ができなくなることは、注意を要する ことである。

（なお、計算ツールは N 及び A カウンタ の ビット数による制限までは 考慮していない）。

■　6.  むすび

以上、PLL の プログラマブル・デバイダ として 現在 最も多く用いられている ２モジュラス・プリスケーラによるパルス・スワロ・カウンタ の 動作 原理 と その使用上の 注意点 を 記した。

また、２モジュラス・プリスケーラによるパルス・スワロ・カウンタ の トータル分周比 N t を得るための 各カウン タ N , A, P の関係を求める 計算ツール を設置した。。

PLL の プログラマブル・デバイダ として 現在 最も多く使用されているのは デュアル モジュラス・プリスケーラ を用いた パルス・スワロ・カウンタ によ るものであると記したが、最近では Delta-Sigma アーキテクチャ による Fractional 分周 を用いた PLL IC チップ が増えている。
数年前までは、Delta-Sigma Fractional PLL を組むには、電力 と 回路規模の増加が課題となっていたが、今 では SSOP チップ で出されている時代となったが、これを 使いこなす、特徴を最大限に生かせるように 如何に 用いるかが 重要な 技術 であるとも考える。