 |
スペアナの基本回路と その動作原理 |
SpaNote |
あらまし オシロスコープが 現象の時間的な特性を表示し、スペクトラム・アナライザ が 現象
の周波数特性を表示する機器であることは 言うまでもない。
そして、時間と周波数の関係は きわめて簡単であり、一方は 他方の 逆数 である。
しかしながら、時間経過という自然現象の中で 暮らす わたしたちにとって、オシロスコープ の基本構成は それとすぐに理解できるが、一方 スペクトラム・
アナライザ スペアナ の場合には、入力は 時間領域であるが、計算 または アナログ演算を行ってから 入力信号の周波数特性を得て
いるので、その基本構成を すぐに理解することは 難しい。
ここでは、掃引スパーヘテロダイン方式による スペアナ の基本回路とその動作原理を記し、どのようにして 周波数軸の スペクトラム線が表示される
かを説明し、スペアナ各部における 主要な性能 を列挙する。
■ 1. スペアナの基本構成図
現在の RF.帯の スペアナ は、フィルタを固定して周波数軸を掃引する スパーヘテロダイン方式である。 図-1 は、この方式の スペアナ の基本
構成 を示す。
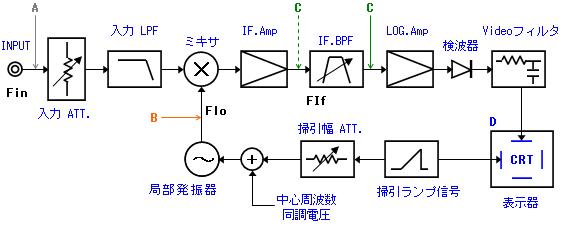
|
| 図-1. スペアナの基本構成図 |
ここで、局部発振器 の信号とミキシングされ、IF.周波数に変換され、IF.バンドパスフィルタ によって必要な分解能によって帯域制限される。
そして、ログ・アンプ によって表示ダイナミック・レンジを確保し、検波器 で RMS検波され、ビデオ・フィルタ によって 雑音を除去したあと、表示の ための CRT へと 導かれる。
また、CRT へは 掃引ランプ信号 が 加えられるが、これと同期して 局部発振器 も掃引することになる。
■ 2. スペクトラム線が表示される動作原理
では、図-1.に記した スペアナの基本構成図において、どのような仕組みで 周波数軸の スペクトラム線が表示されるのか。
図-1.の掃引スペクトラム・アナライザ の パラメータを次の値として 解析してみる。
・ 入力信号 Fin の周波数範囲は、直流から 100KHz とする。
・ 掃引局部発振器の周波数 Flocal は、 250KHz から 350KHz まで掃引する。
・ IF.周波数 FIf は、250KHz として 分解能帯域幅は 10KHz 程とする。
なお、図-1.に記す A , B , C 箇所を モニターするとして 図-2.にその動作波形を示す。
すると ミキサ において 局部発振器の周波数とミキシングされ 次の3つの式に示す信号が生まれる。
・ FIf = Flocal + FIn
・ FIf = Flocal - FIn
・ FIf = FIn + Flocal
次に、2番目の式を用いて (ここでは スペアナの周波数構成を上側ヘテロダイン、局部発振器の周波数を入力信号より FIf だけ高い 周波数として)、動作を説明する。
まず、スペアナの入力信号 Fin 30KHz と 70KHz の信号を スペアナの表示器 CRT に 0 から 100KHz のスパンで表示 するために、局部発振器 Flocal は、250KHz から 350KHz で掃引させなければならず、 図-1. の構成図の 掃引ランプ 信号と掃引幅ATT. と中心電圧同調電圧 によって 局部発振器を制御してなされる。
今、この状態で 30KHz の Fin 信号が CRTに表示されるには、Flocal が 250KHz から掃引 スイープ し始めて Fin より FIf だけ高い周波数の時、図-2. に示すごとく すなわち、Flocal が 280KHz 時にFIfの周波数は 250KHz となり帯域フィルターを通過して表示されることになる。
また、同様に 70KHz の Fin 信号が CRTに表示されるには、 Flocal が 320KHz 時 となる。
さらに、もう 1つ FIf の周波数が 250KHz となる場合がある それは、 Flocal 自身が 250KHz を発振する時であり、これを ローカル・フィードスルー または 俗に ゼロ・キャリア と呼び、ヘテロダイン スペアナ に付き物 の スプリアス である。
そして、ここで注意したいのは 例えば Flocal が 270KHz 時は どうなるかと言うことで、FIf = 270KHz - 30KHz で FIfの周波数 は 250KHz とならないが、 実際には、図に示す如く IF. の帯域フィルター を通過 し、CRT 表示に出力が表れることである。
ということは、スペアナに表示されるスペクトラムの形状は、IF.フィルターの周波数特性にほかならない。
試しに、Flocal を 掃引 させて見ると、入力には 30KHz と 70KHz の この 場合 直線で表したスペクトラムなのに CRT には IF.フィルターの形状の出力がされることになる。
もし、入力信号の周波数差が 10KHz 程であれば このスペアナでは 全く 2つの信号を分解して観測できないということで、スペアナの周波数分解能 は、この IF.帯域幅で決まることになる。
■ 3. スペアナ各部の主な性能
次に、スペアナの各部、各回路の性能が スペアナのどの特性を 主に左右するかを 簡単に列挙する。
入力アッテネータ
入力アッテネータの特性は スペアナの レベル測定確度、広帯域のスペアナになるほど その周波数特性、また スペアナの
最大入力電力を制限する。
入力ローパスフィルタ
入力LPF. も非常に重要な回路であり、先ほど述べた ローカル・フィードスルー や IF.フィードスルー が、上のスペアナ例では 250KHz の
信号が スペアナの入力端子から放出するのを防いでおり、また イメージ応答を軽減する役目もある。
ミキサ
ミキサ 自身の性能が スペアナの ダイナミック・レンジ、測定確度、周波数特性 に大きく影響し、さらに 2次歪み や 2信号3次歪み の 特性をも左右する。
IF.フィルタ
先に述べたように IF.フィルタ によって 周波数分解能 が決定され、さらに この帯域幅によって スペアナの掃引スピードが決まる。
IF.フィルタ は 時定数を持つため、掃引時には これが十分に応答できる時間を与えなければならない。 ゆえに、分解能を上げた測定ほど 時間が
かかることになる。
LOG Amp. 対数増幅器
スペアナの 表示ダイナミックレンジ は、対数増幅器の LOG.圧縮性能に左右され、振幅表示確度や直線性 に影響を及ぼす。
(人の目と脳は、対数圧縮をたやすく行っている。 例えば、ゾウ と アリ の大きさを比べる時に 瞬時にゾウを圧縮したスケールで 考える
ことができるが、対数増幅器もこれと 同じことをおこない、ゾウ のような信号と アリ のような信号を同じスケールで見ることができる)。
検波器
ここで、IF.周波数を 検波 して、DC.からの成分へと変換するのだが、ここでも その検波器の ダイナミックレンジ や 直線性が 直接 スペアナの 表示
ダイナミックレンジ や 振幅表示確度 に影響を及ぼすことは言うまでもない。
また、通常 検波回路は 平均値検波であり、それを RMS.値に 値付けしている。
局部発振器、周波数シンセサイザ
局部発振器 やはりこれは スペアナ の心臓です。 周波数測定確度 はもちろん 周波数安定度 は この局部発振器の性能と
なり、これらを向上するために 周波数シンセサイザ は 高安定な クリスタル発振器と PLL フェイズロック技術を用いて構成されることになる。
局部発振器 Local がもつ位相雑音も 大きな問題となり、Local に存在する位相雑音は 同じ比率で IF.の受信信号に現れる。 例え
ば、Local キャリア から -90dBc/Hz の位相雑音は 受信信号にも -90dBc/Hz として現れ、この雑音より 小さな信号は うもれてしまうことになる。
■ 6. むすび
以上、掃引スパーヘテロダイン方式による スペアナ の スペクトラム線がどのようにして表示されるかを簡単なスペアナの
モデルを使って説明した。
そして、スペアナに搭載されている主要な回路についても その概要を記した。
スペアナは、様々な RF.や アナログ技術を結集して作られており、また その測定機としての応用範囲も非常に広い。
ここでは、簡単なスペアナの構成図だけを示したが、実際の RF.帯 スペアナ や TG. トラッキング・ジェネレータ を 付加した構成や 動作原理等は 別に まとめる ことが
できれば と考えている。